84. Largest Rectangle in Histogram

problem description

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

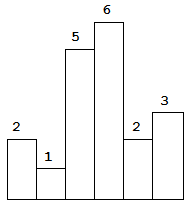
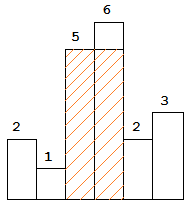
Input: [2,1,5,6,2,3]
Output: 10

algorithm thought

一次遍历解决问题，使用栈来辅助解决。对于数组，如果碰到顺序递增，就将当前数字压入栈中，如果当前height小于栈顶值，就将栈顶值弹出，并计算以弹出值为高度的矩形面积大小。这里关键是如何去计算矩形的宽，根据我们之前的算法，可以知道，当前栈顶的值肯定代表的是当前访问过的，剩下的最大值，因为比他更大的值在之前肯定被弹出计算了，那么，可以用当前index减去当前栈顶代表的index，就能表示矩形的宽了。

code

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> st;
        heights.push_back(0);
        int res=0;
        for(int i=0;i<heights.size();){
            if((st.empty())||heights[i]>=heights[st.top()]){
                st.push(i);
                ++i;
            }else{
                int t=st.top();st.pop();
                if(st.empty()){
                    //cout<<heights[t]<<'-'<<i<<' ';
                    res=max(res,heights[t]*i);
                }else{
                    //cout<<heights[t]<<'-'<<i-st.top()-1<<' ';
                    res=max(res,heights[t]*(i-st.top()-1));
                }
            }
        }
        return res;
    }
};

algorithm analysis

使用栈，一次遍历得到结果，时间复杂度O(n)